≣ Contents

LYC-MATH는 온라인 수업을 기반으로하야 전국의 수험생들을 대상으로 100% 커스터마이징된 첨삭 서비스를 제공합니다. 어디에 질문해야할지 몰랐던 디테일한 질문들, 정확히 내가 궁금한 부분을 긁어줄 수 있는 포인트 강의를 고객님과의 상담을 통해 제공해드리고 있습니다. 글 가장 하단에 카카오톡 문의 채널이 있으니 부담없이 문의주세요!
2024학년도 고3 수능 22번
문제 소개 - 2024학년도 고3 수능 22번

- 출제 범위 및 단원 : 수학2 미분의 활용
- 문제 닌이도 : 상
- 문제에서 요구하는 교과 개념 : 미분의 활용
문제 해설 - 2024학년도 고3 수능 22번


포인트 1. 문제 평가
오랜만에 다소 생소하고 어려운 문제가 나왔다고 생각합니다. 기존에 나오던 문제들과는 약간 다른 스타일의 문제여서 접근 방법 자체에서 고민이 많지 않았을까 하는 생각이 듭니다. 기본적으로 f(정수)들에 대한 생각을 할 수 있어야만 그 다음 생각들을 만들어갈 수 있다는 점이 문제의 난이도를 더 올리지 않았나 생각해봅니다.
이 문제는 겉보기에는 별 거 아닌 문제처럼 보일 수 있지만, 사실 기존의 스타일과 다르기 때문에 그 접근법 자체를 찾는 것에서 난이도가 있는 문제입니다. 따라서 여러분들도 앞으로 이런 f(정수)들의 부호들에 대한 문제라면 이러한 접근법을 생각해보는 것도 좋을 것 같습니다.
포인트 2. 핵심이 되는 생각
저도 이 문제를 연구하면서 이런 풀이 저런 풀이를 고민해보고, 다른 사람들이 풀어놓은 것도 찾아보고 했습니다만, 역시 아무래도 핵심이 되는 생각은 이것인 것 같습니다.
연속된 음수값들과 연속된 양수값들의 경계
최고차항이 양수인 삼차함수의 특징상 왼쪽 어딘가에는 f(정수)들이 계속 음수의 값을 가질 것이고, 오른쪽 어딘가에는 f(정수)들이 계속 양수의 값을 가질 것 입니다. 그렇다면 언젠가 그 흐름이 깨지는 순간이 있을 것인데, 그 흐름이 깨지는 순간이 단순히 음음음양양양 으로 깨진다면 문제의 조건을 만족할 수 없다는 것을 알 수 있습니다.
결국 음음음 - - - - - - 양양양 으로 전개된다면 ----- 부분에 어떤 일이 일어나야 문제의 조건을 만족할 지 생각해보아야 합니다. 그런데 이때 정말 핵심이 되는 개념이 이것이지요.
포인트 3. 연속된 음수의 마지막과 연속된 양수의 마지막
문제의 제 영상 해설이나 위에 사진 풀이에서도 보이고 있습니다. 파랑색으로 표시해 놓았지요. 저 연속된 음수의 마지막 값이라는 개념 때문에 그 전에 있던 음수값은 그 다음다음에 나올 값과의 관계를 생각해볼 때, 0일 수 밖에 없다는 결론을 얻습니다. 이것은 오른쪽에 연속된 양수값들에서도 같은 결과를 얻을 수 있습니다.
이것으로 우리는 일단 음음음 양양양 사이에 적어도 두 개의 정수근이 있다는 사실을 확인할 수 있습니다. 이 사실로부터 이제 일반적인 문제풀이의 궤도에 올려놓을 수 있습니다.
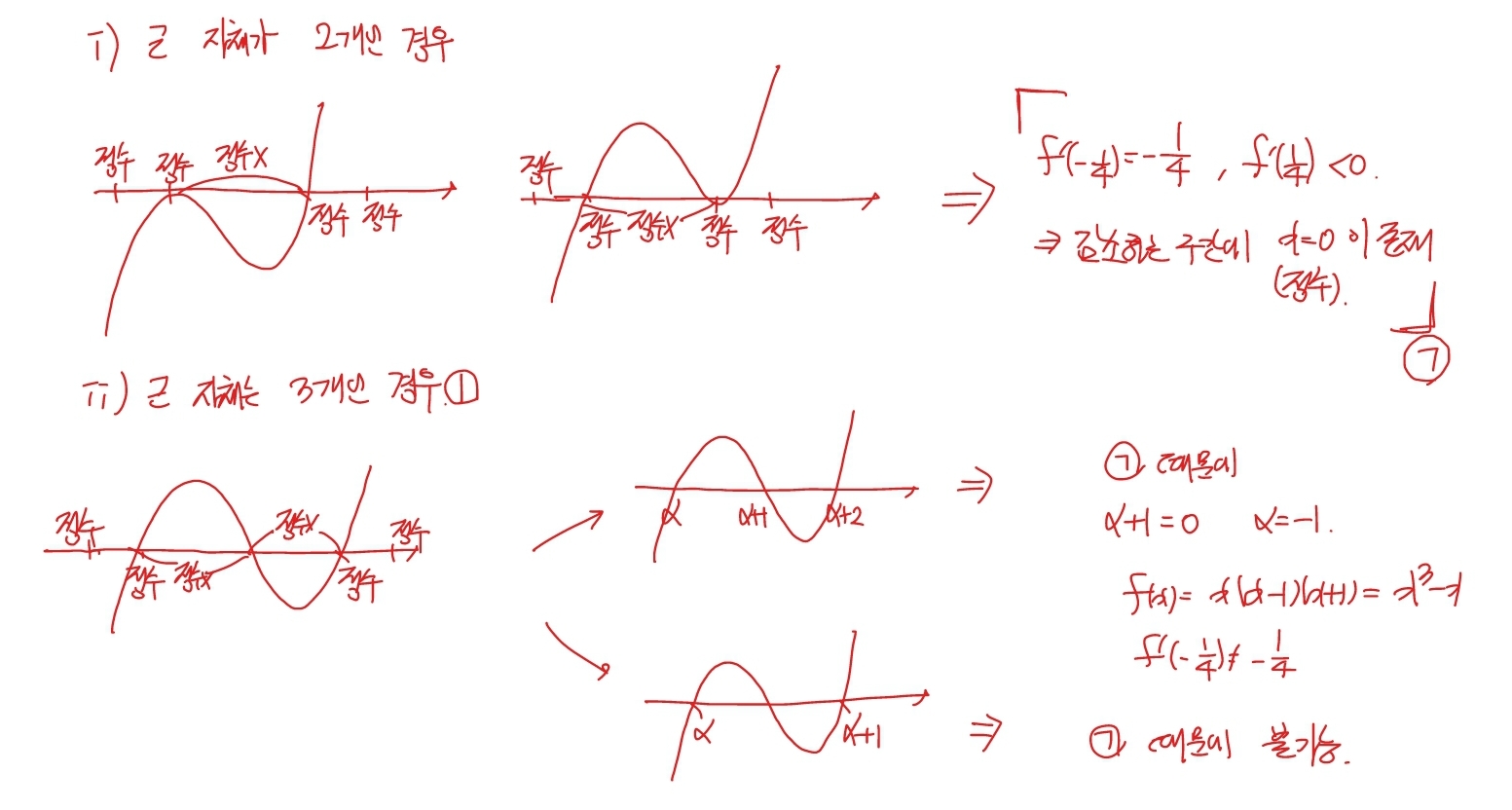
지금부터 가능한 여러 가지 경우들을 살펴봐야 할 차례입니다. 먼저 일단 삼차함수가 x축이랑 적어도 2개의 점에서는 만나는 것이니, 삼차함수가 x축이랑 만나는 점 자체가 2개인 경우를 살펴봅니다. 그런데 이 과정에서 이 문제의 두 가지 핵심 포인트에 또 다가가게 됩니다.
포인트 4. 구간에 정수가 있냐 없냐, 그리고 f '(-1/4)=-1/4와 f '(1/4)<0의 사용
경우를 따짐에 있어서 x축과의 교점에 정수근을 놓게 되는데, 왼쪽 근을 기준으로는 한 칸 더 왼쪽에도 정수값이 있고, 오른쪽 근을 기준으로는 한 칸 더 오른쪽에도 정수값이 있습니다. 이때 지금 언급한 정수값은 2칸 떨어져서 있는 정수값과 곱해서 음수가 되면 안되는 상태들입니다. 따라서 두 개의 정수근 사이에 또 다른 정수가 있게 되면 이 상태를 만족할 수 없다는 결론이 나옵니다.
그래서 두 개의 정수근은 어쩔수 없이 연속한 정수가 됩니다. 이때 f '(-1/4)의 값과 f '(1/4)의 값이 의미를 가질 순서 입니다. 분명히 f(x)는 x=-1/4부터 x=1/4까지 감소하고 있습니다. 이때 중요한 것은 -1/4과 1/4 사이에는 0이라는 정수가 있다는 점입니다. 다시 말해, f(x)는 감소하는 구간에 정수 0이 한 번 있습니다.
이러한 사실에 의해서 f(x)가 x축이랑 두 점에서 만나는 경우는 불가능한 것을 알 수 있습니다. 방금 우리가 두 개의 정수근은 연속한 정수라는 결론을 냈는데, 그럼 그 사이에 감소하는 구간에는 0이라는 정수가 조재할 수 없기 때문입니다. 여기서 사용한 이 개념은 뒤에 문제풀이에도 계속 이용될 개념이기 때문에 ㄱ 이라고 칭하겠습니다.
이제 이 문제를 풀어가는데 필요한 개념은 모두 설명이 끝났습니다. 지금까지 소개해드린 개념으로 나머지 풀이를 보게되면 빠르게 이해가 갈 것 입니다.
이제는 두 번째 케이스인 f(x)=0의 근은 3개인 경우를 살펴봅니다. 이때 정수근이 세 근 중 양 끝에 있는 경우를 먼저 보는데, 이 경우 마찬가지 이유로 두 개의 케이스로 구분 됩니다. 연속된 세 개의 정수근을 갖는 경우와 두 개의 연속된 정수근 사이에 정수근이 아닌 다른 근이 있는 경우입니다.
첫 번째 경우는 식을 만들면 f(x)=x(x-1)(x+1)인데, 이것은 f '(-1/4)=-1/4을 만족하지 못해서 불가능합니다. 두 번째는 ㄱ의 상태를 만족하지 못하므로 불가능합니다.
마지막 세 번째 케이스는 정수근이 가운데와 오른쪽, 가운데와 왼쪽 근이 되는 상태입니다. 각각의 경우 모두 같은 논리로 두 개의 정수근은 연속된 근일 수 밖에 없습니다. 그리고 나머지 하나의 근은 풀이에서 동일하게 네모로 두았으며, 그 네모의 값은 1 차이보다 적게 나야 하는 상태입니다. 이것을 조건에 적용하면 네모의 값은 0에서 1사이의 값을 가져야 합니다.
이 조건이 마지막 답을 내는 조건인데, 왜냐하면 지금 만들어지는 두 개의 케이스 중에서 f '(-1/4)=-1/4을 계산하면 네모의 값을 얻을 수 있는데, 이 네모의 값의 범위를 이용하여 최종적인 한 케이스를 특정짓게 됩니다.
LYC-MATH-HWW 소개
LYC-MATH_HWW는 현장에서 16년간 중고등학생들과 소통하며 강의를 해온 수학 강사입니다. 이제는 단순히 수학이라는 지식을 전달하는 것을 넘어서 수학을 어떻게 공부해야하는지, 수학을 어떻게 가르쳐야 하는지를 강의하고 있습니다. 또한 다년간의 빅데이터를 바탕으로 학생들이 A의 상황에서 어떤 생각을 가지고 있는지 그 뿌리부터 이해하여 근본적인 솔루션을 제공하고 있습니다. 아래는 LYC-MATH가 제공하는 서비스 목록입니다.
1. 100% 커스터마이징 온라인 첨삭.
수학을 공부하며 도움이 필요한 모든 개개인의 사항에 대하여 고객맞춤의 도움을 드리고 있습니다. 서비스는 온라인으로 진행되며, 실시간 온라인 소통 방식 또는 요청하신 내용의 강의 제작 방식으로 진행할 수 있습니다.
2. 수학 공부법 개인 첨삭
현장에서 강의를 하다보면 정말 많은 학생들이 열심히 해도 잘 할 수 없는 방식으로 공부하고 있는 것을 볼 수 있습니다. 수학은 정확히 공부하는, 그리고 생각하는 방법이 있으며, 그 방식으로 반복 훈련하면 금방 습관화시키고 자연스럽게 터득하게 됩니다. 학습자의 상황에 맞춰서 개선해야 하는 부분을 제시하고, 그 부분을 습관화시키기까지 서비스를 진행합니다.
3. 온라인 개인 과외
중고등 학생을 대상으로 필요한 과정에 대한 개인 과외도 진행하고 있습니다.
아래 유튜브 채널 링크를 통해서 운영중인 채널에 올라와 있는 다양한 강의들을 찾아보실 수 있습니다.
또한 네이버 블로그에서 학생들이 남겨진 강의 후기, 공부법 강의 후기 등을 찾아보실 수 있습니다.
또한 기타 궁금하신 사항은 카카오톡 오픈 채팅을 통해서 상담 도와드리고 있으니 편하게 문의 주시면 감사하겠습니다.
| lyc-math 유튜브 채널 | lyc-math 네이버 블로그 | 카카오톡 오픈 채팅 |
 |
 |
 |
'수능 및 평가원 모의평가 기출 해설 > 2025학년도 수능 수학' 카테고리의 다른 글
| 2024학년도 수능 미적분 28번 해설 (0) | 2025.04.17 |
|---|---|
| 2024학년도 수능 미적분 27번 해설 (0) | 2025.04.15 |
| 2024학년도 수능 수학 확률과 통계 29번, 30번 해설 (0) | 2025.04.08 |
| 2024학년도 고3 수능 수학 확률과 통계 27번, 28번 해설 (0) | 2025.04.04 |
| 2024학년도 고3 수능 수학 21번 해설 (0) | 2025.03.28 |
| 2024학년도 고3 수능 수학 20번 해설 (0) | 2025.03.26 |
| 2024학년도 고3 수능 수학 15번 해설 (0) | 2025.03.21 |
| 2024학년도 고3 수능 수학 14번 해설 (0) | 2025.03.20 |





