반응형
수학1의 주요 개념 ‘원리합계’를 완벽히 정리했습니다. 공식과 뜻, 수능 기출 활용 방법까지 예시와 함께 배워보세요. 원리합계는 등비수열의 응용 중에서도 실생활과 가장 밀접한 수학1 개념입니다. 기수불/기말불 구분과 함께 적금·예금 계산 문제를 완전 정리해드립니다.

≣ Contents
원리합계에 대한 개념과 핵심
1. 원리합계란?
원리합계는 일정한 금액을 매년 저축하면서 이자(복리)를 더해 나중에 통장에 쌓이는 총액을 의미해요. 이 개념은 수학적으로는 등비수열의 합 공식으로 처리할 수 있습니다.
2. 연이율과 복리 이해하기
- 연이율 r: 1년 동안 통장에 있는 돈에 붙는 이자의 비율
예) 연이율이 5%일 경우 → 원금의 5%인 5,000원이 붙음 - 복리: 이자가 원금에만 붙는 게 아니라, 붙은 이자에 대해서도 다음 해에 또 이자가 붙는 방식
예) 10만 원을 넣으면 →- 1년 후: 10만 × 1.05 = 10.5만 원
- 2년 후: 10.5만 × 1.05 = 11만 원
3. 기수불과 기말불의 차이
- 기수불: 매년 초에 돈을 넣는 것 → 초항에 이자가 한 번 더 붙음
- 기말불: 매년 말에 돈을 넣는 것 → 초항 그대로, 마지막 해에 처음으로 이자 적용됨
예를 들어, 연이율 10%로 a원을 3년 동안 넣을 경우:
A (기수불)
- a(1.1)³ + a(1.1)² + a(1.1)
B (기말불)
- a(1.1)² + a(1.1) + a
기수불은 매번 이자가 조금 더 많이 붙는 구조이기 때문에 총합이 더 큽니다.
4. 원리합계 공식
① 기수불 (매년 초에 저축)
- 초항: a(1 + r)
- 공비: (1 + r)
- 항 수: n개

② 기말불 (매년 말에 저축)
- 초항: a
- 공비: (1 + r)
- 항 수: n개

Tip:
- 이율이 15%라면 공식에 들어가는 r은 0.15
- 퍼센트가 아닌 소수 형태로 대입해야 함
원리합계 예제
예제 1
연이율 6%, 1년마다 복리로 매년 초에 30만 원씩 저축할 때, 10년 후의 원리합계를 구하여라. (단, 1.06¹⁰ = 1.8)
- 연이율 r = 0.06
- 공비 = 1.06
- 초항 = 30 × 1.06
- 공식:

예제 2
연이율 12%, 매년 말에 100만 원씩 저축할 때 10년 후 원리합계를 구하라. (단, 1.12¹⁰ = 3.1)
- 초항 = 100
- 공비 = 1.12
- 공식:
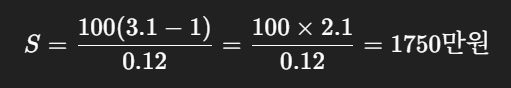
원리합계 포인트 정리와 확인 예제
- 원리합계는 등비수열을 바탕으로 이자 복리 효과를 적용한 모델
- 기수불과 기말불의 구분이 핵심이며, 이를 잘못 판단하면 계산이 틀어짐
- r은 %가 아닌 소수(예: 10% → 0.1)로 바꾸어 공식을 적용해야 함
- 예금, 적금, 수능 실전 문제 등에서 다양하게 응용됨
확인 예제. 답은 4번입니다~

LYC MATH 개념 강의 보러 가기
반응형
'중고등 및 수능 수학 개념 정리 > 고등 수학 개념 정리' 카테고리의 다른 글
| 수열의 합 시그마 중급 개념 - 수학1 (0) | 2025.06.02 |
|---|---|
| [공통수학1] 부정방정식 푸는법 총정리 – 정수 조건과 실수 조건 해설까지 (0) | 2025.05.19 |
| 대칭형의 연립이차방정식 - 공통수학1 (0) | 2025.05.09 |



