시그마 계산이 막막하다면 꼭 알아야 할 핵심 개념 3가지! 시그마의 성질, 기본 공식 활용법, 일반항 찾는 법까지 수학 강사 관점에서 정리했습니다.

≣ Contents
너가 꼭 기억할 결론
- 시그마는 ‘넣고 더하는’ 것이다. 모르면 일단 손으로 써보자.
- 위끝·아래끝을 조절하여 시그마 식을 변형할 수 있다.
- 시그마 공식을 외울 게 아니라, 식의 의미를 이해해야 한다.
- 합을 구하려면 일반항이 반드시 필요하다. 일반항은 관찰을 통해 찾는다.
수열의 합 시그마 중급 개념 첫 번째.
시그마의 위끝,아래끝을 조절하는 방법
시그마는 단순히 기호가 아니라, 넣고 더하는 ‘과정’이다.
예를 들어,

처럼 두 개의 시그마를 하나로 합칠 수 있다. 이때 중요한 건 경계가 이어지는가이다. 3 다음엔 4가 와야 한다.
반대로 뺄 수도 있다.

이건 생각해 보면 당연하다. ‘넣고 더하는’ 구조를 그대로 따라가면 되는 것! 또 하나! 시그마 공식을 쓰기 위해선 아래끝이 1부터 시작해야 한다. 예를 들어,

이렇게 위끝과 아래끝을 ‘조작’하여 공식을 적용할 수 있도록 만드는 게 핵심이다.
수열의 합 시그마 중급 개념 두 번째.
시그마 공식은 결과가 아니라 과정으로 외워야 한다.
많은 학생들이

이건 외우는데,

이걸 못 본다. 이건 공식 외우기가 아니라, 시그마의 본질을 놓친 것이다.
수열의 합 시그마 중급 개념 세 번째.
합을 구하려면 일반항을 먼저 찾아야 한다.
수열의 합을 구하는 문제에서 가장 먼저 해야 할 일은? 일반항을 찾는 것이다. 예를 들어,
수열: 2×1, 4×4, 6×7, 8×10 …
→ 앞 숫자: 2, 4, 6, 8 → 2n
→ 뒤 숫자: 1, 4, 7, 10 → 3n - 2
→ 일반항: an = 2n(3n - 2)
이걸 통해 합을 구할 수 있는 시그마 식을 만든다.
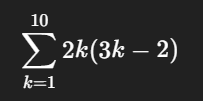
기본공식으로 풀 수 있게 전개해서 계산하면 된다. 또 어떤 경우엔 일반항 자체가 ... 구조일 수도 있다.

이럴 땐 ‘합을 다시 합하는 문제’이므로, 시그마 안에 시그마가 들어가기도 한다. 이럴 때는 반드시 ‘압축’해주는 과정이 필요하다.
예:

수열의 합 시그마 중급 개념 정리
- 시그마는 “넣고 더하는 것”이라는 개념을 바탕으로 접근해야 한다.
- 위끝·아래끝을 조절하면 여러 시그마 식을 결합하거나 나눌 수 있다.
- 시그마 공식은 결과가 아니라 ‘의미’를 이해하고 외워야 한다.
- 합을 구하기 위해선 일반항부터 만들어야 하며, 일반항이 ∑ 구조일 경우엔 다시 공식으로 압축해야 한다.
- 등차/등비 수열 뿐 아니라 규칙성 관찰을 통해 일반항을 직접 유도하는 능력이 중요하다.
LYC MATH 개념 강의 보러 가기
'중고등 및 수능 수학 개념 정리 > 고등 수학 개념 정리' 카테고리의 다른 글
| 원리합계 - 수학1 (개념, 예제, 인강까지 한 번에) (1) | 2025.05.29 |
|---|---|
| [공통수학1] 부정방정식 푸는법 총정리 – 정수 조건과 실수 조건 해설까지 (0) | 2025.05.19 |
| 대칭형의 연립이차방정식 - 공통수학1 (0) | 2025.05.09 |



