평행사변형의 조건은 단순히 ‘그림 보고 느낌대로’ 푸는 문제가 아닙니다. 반드시 외워야 할 5가지 조건과 간접 표현까지 정확히 파악해야 문제에서 틀리지 않습니다. 이 글을 통해 그 원리와 예제 해설까지 확실히 정리해보세요.

≣ Contents
평행사변형이 되는 조건에 대한 개념과 핵심
꼭 기억할 핵심 개념
- 평행사변형이 되는 조건은 총 5가지이며 반드시 외워야 한다.
- 문제에서 조건이 간접적으로 표현되기도 하므로 해석 연습이 필요하다.
- 조건에 해당하는지를 판별 기준으로 삼아야 하며, 그림 보고 느낌으로 풀면 안 된다.
- 대표적인 간접 표현: 동의각이 같음 → 평행함, 대각의 합이 같다 → 각의 크기가 같다 등.
- 정확한 조건을 찾아내는 것이 ‘진짜 수학적 사고’다.
기본적인 공부 방법
평행사변형의 조건 5가지, 이건 무조건 외워야 한다
평행사변형이 되는 5가지 조건
- 두 쌍의 대변이 서로 평행
- 두 쌍의 대변의 길이가 같다
- 두 쌍의 대각의 크기가 같다
- 대각선이 서로를 이등분한다
- 한 쌍의 대변이 평행하고 길이도 같다
이 다섯 가지 중 하나라도 성립하면 그 사각형은 평행사변형입니다. 따라서 문제는 ‘이 다섯 가지 중 어떤 조건에 해당하는가’를 찾는 연습으로 접근해야 합니다.
“헷갈리게 낸다”는 말은 결국 간접 표현이 많다는 뜻
문제에서는 평행이라는 말을 동의각, 엇각이 같음 같은 간접 표현으로 제시하기도 합니다. 이런 표현을 보면서 “아, 이건 평행을 말하고 있구나” 하고 해석할 수 있어야 해요.
예를 들어, 어떤 각이 60도고 다른 각이 120도일 때, 이게 단순한 숫자 비교가 아니라 동의각이 같다는 간접 표현일 수 있습니다. 그럼 그 두 직선은 평행하고, 거기에 길이 조건까지 주어지면 조건 5번(한 쌍의 대변이 평행하고 길이가 같다)이 성립되는 거죠.
평행사변형이 되는 조건 예제
예제 1
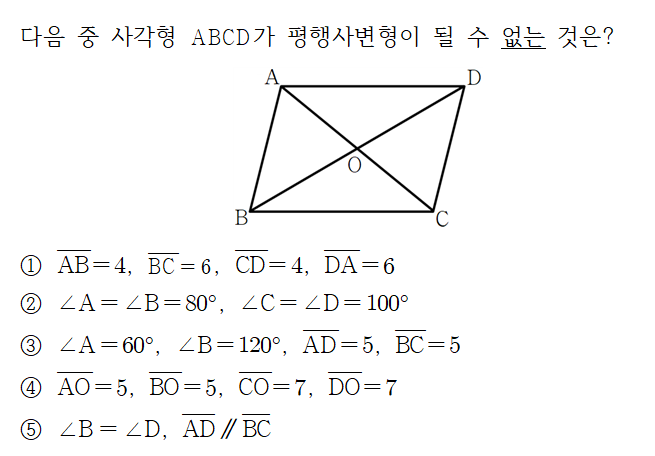
보기 1
“네 변의 길이가 각각 4, 6, 4, 6이다”
→ 두 쌍의 대변의 길이가 같음 → 조건 2번 → 평행사변형 O
보기 2
“각의 크기가 80, 80, 100, 100이다”
→ 단순히 각이 같다고 해서 조건 성립 X → 조건 없음 → 평행사변형 X
보기 3
“어떤 각이 60도, 맞은편이 120도, 길이는 각각 5씩”
→ 동의각이 같다는 간접 표현(동각 60, 120 → 보각으로 평각 형성)
→ 평행 + 길이 같음 → 조건 5번 성립 → 평행사변형 O
보기 4
“대각선 길이가 각각 5, 7로 다르다”
→ 대각선이 서로 이등분하지 않음 → 조건 없음 → 평행사변형 X
보기 5
“각 B와 D가 같고, 선분AD와 선분 BC가 평행하다”
→ 각 B와 D의 크기를 a라고 두면, 선분AD와 선분BC가 평행하므로 각 A와 각 C의 크기가 각각 180-a로 같음.
→ 조건 3번(두 쌍의 대각의 크기 같음) → 평행사변형 O
평행사변형이 되는 조건 포인트 정리와 확인 예제
문제 푸는 사고방식 자체가 바뀌어야 한다
이 유형은 결국, **‘되는 조건 외우기’ + ‘조건을 찾아내는 눈’**이 핵심입니다. 그림이 어설프게 평행사변형처럼 보인다고 넘어가면 오답이 나올 수 있어요.
정답은 ‘조건을 만족하느냐’에만 달려있습니다.
📌 한 줄 요약:
보이는 대로 풀지 말고, 조건을 통해 판단하자. 그리고 간접 표현도 읽어낼 수 있도록 연습하자.
확인 예제. 답은 4번, 5번입니다~

LYC MATH 개념 강의 보러 가기
https://youtu.be/Eg8WG0RvatA?si=gG8TszNc4rELnZw7
